5학년 2학기 개념 단원 마무리 수학
큐브 수학 076쪽 17번 문제인데요, 질문은 이렇습니다.
두 삼각형은 서로 합동입니다. 삼각형 ㄱㄴㄷ의 둘레가 20cm 일 때, 변 ㅁㅂ은 몇 cm 인가요?
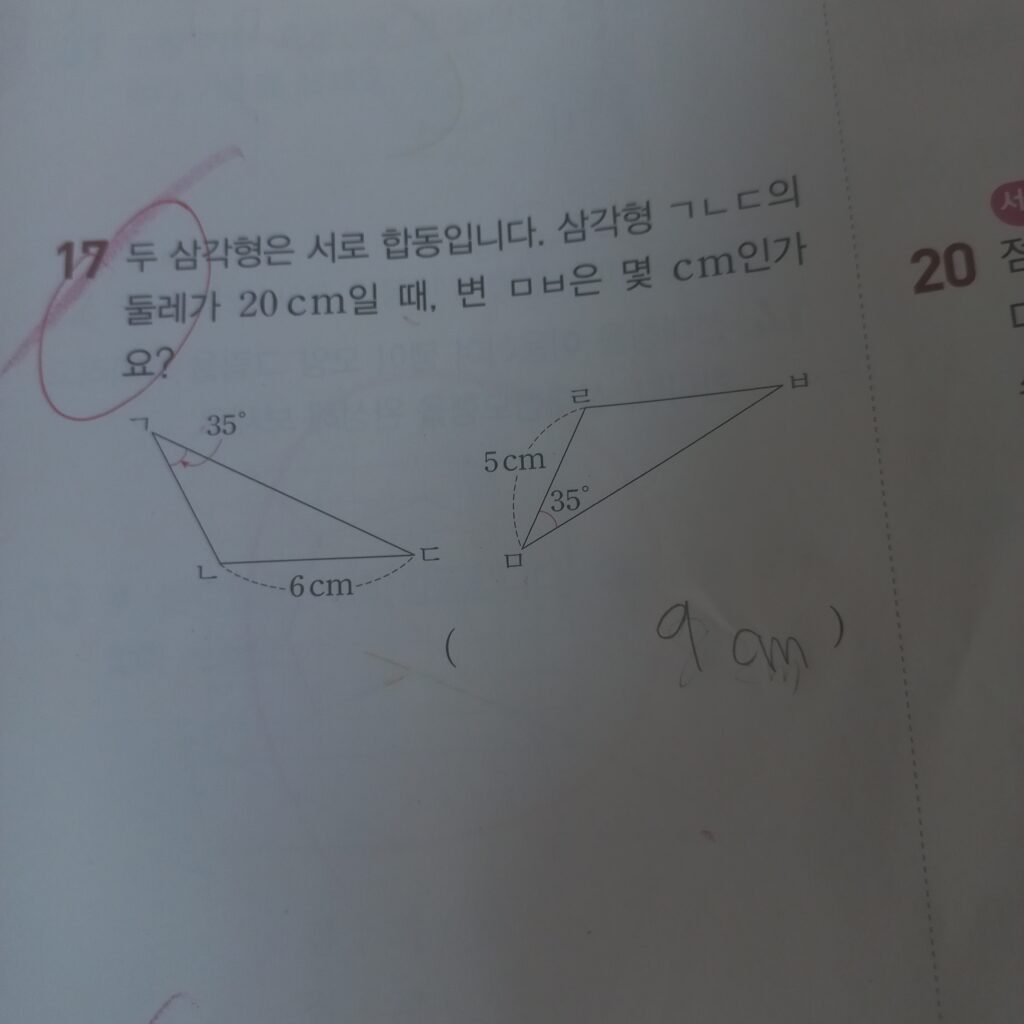
이 문제는 제가 뭘 착각 한것 같습니다. 두 삼각형은 합동이니까 각도, 길이 등 다 같겠네요.
왼쪽 삼각형은 밑변이 6센치, 오른쪽 삼각형은 높이가 5센치라고 나와 있습니다. 여기서 문제를 다시 봅시다.
둘레가 20센치니까 나머지 길이를 구하라는 문제 였는데 , 이제 6더하기 5는 11이니까 20-11=9 즉 답은 9센치 입니다.
18번 문제
직선 ㄱㄴ을 대칭축으로 하는 선대칭도형입니다. 네모안에 알맞은 수를 써넣으세요.
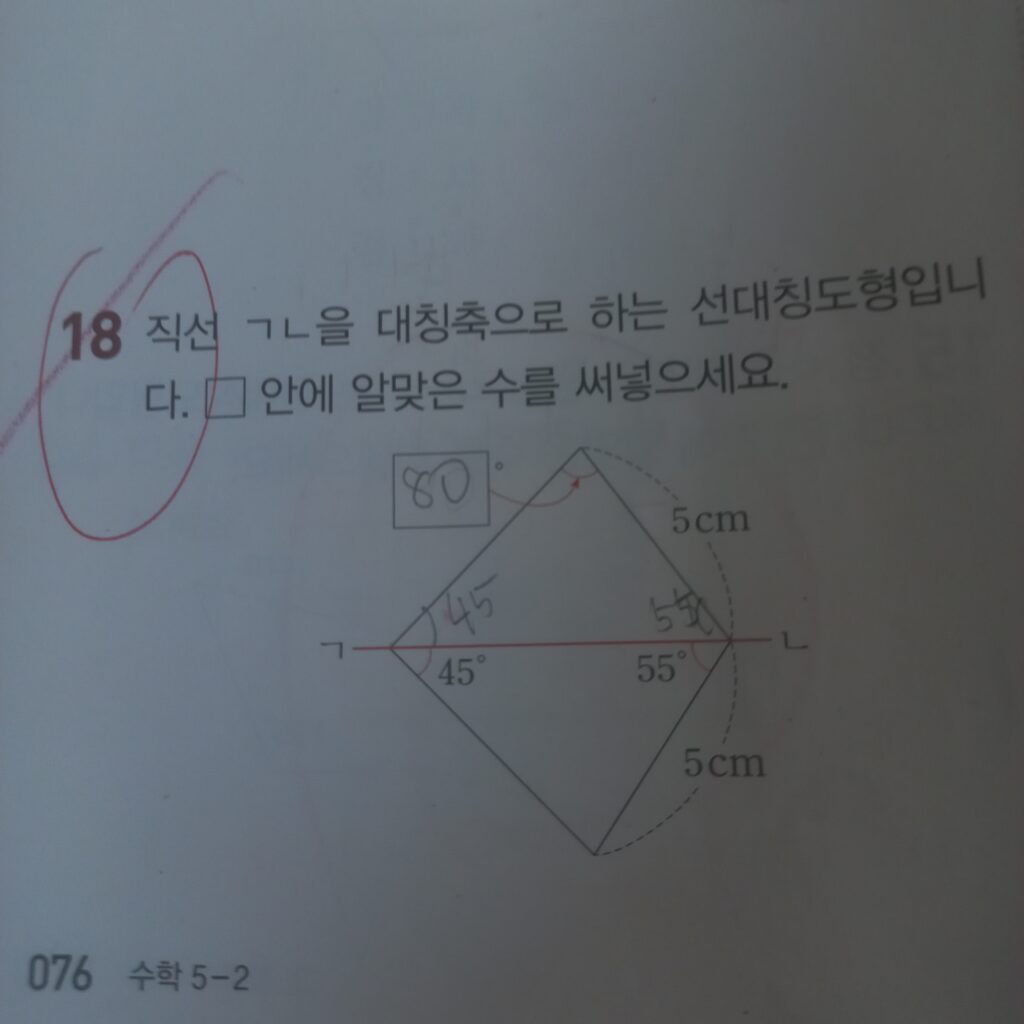
이 문제의 그림을 잘보면 삼각형이 숨어있습니다. 각도를 구하는 문제였는데요, 45도 더하기 55도는 100도,
삼각형 하나의 각도가 180도 니까 답은 80도!
라이트 1학기 복습책 6단원 다각형의 둘레와 넓이
77쪽 8번
사다리꼴과 마름모의 넓이의 차는 몇 제곱센티미터인지 구해 보시오.
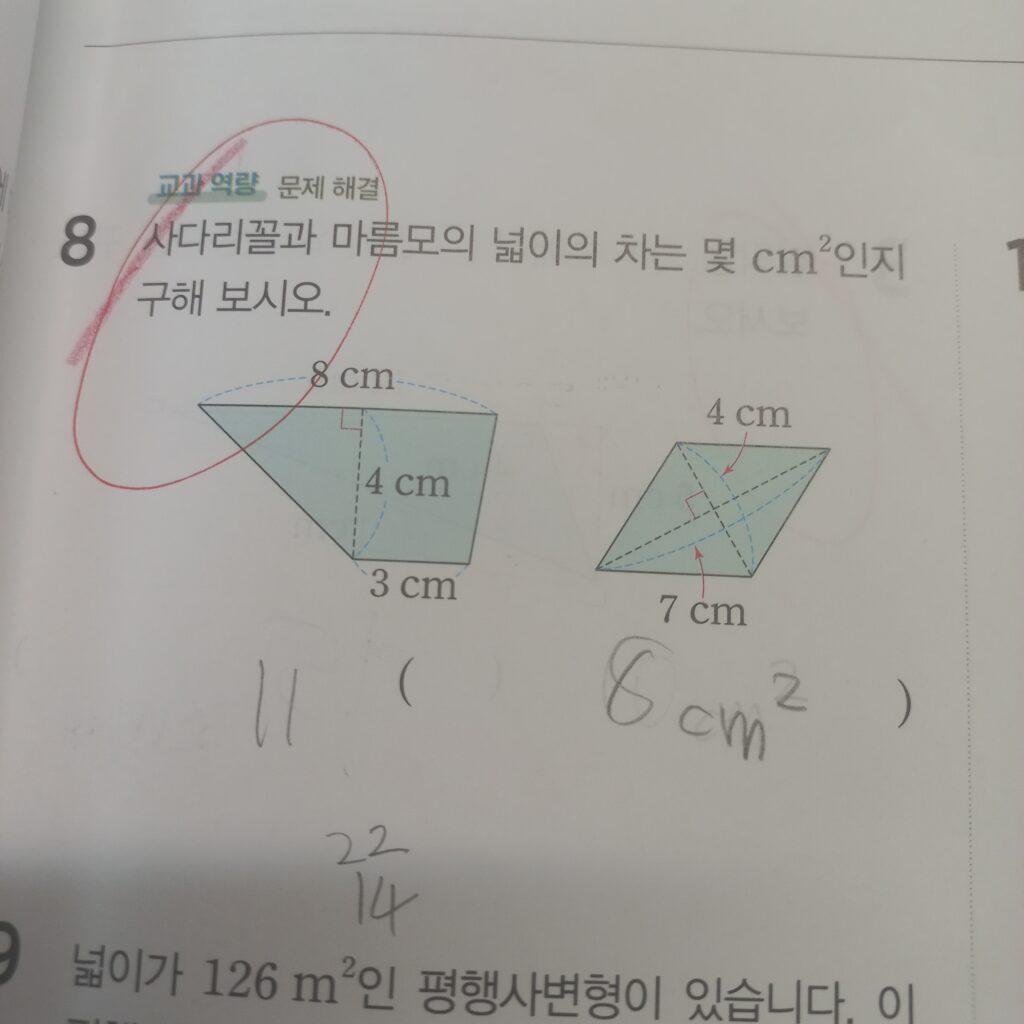
이 문제는 제가 계산실수를 하여 틀렸습니다. 사다리꼴은 윗변의 길이가 8센치, 아랫변은 3센치 , 높이는 4센치 였습니다.
마름모의 한 대각선의 길이는 4였고 다른 대각선의 길이는 7이었습니다. 이제 전체적으로 구하면
22-14=8 8제곱센티미터
78쪽 응용문제 3번
삼각형 ㄱㄴㄷ에서 네모안에 알맞은 수를 구해 보시오.
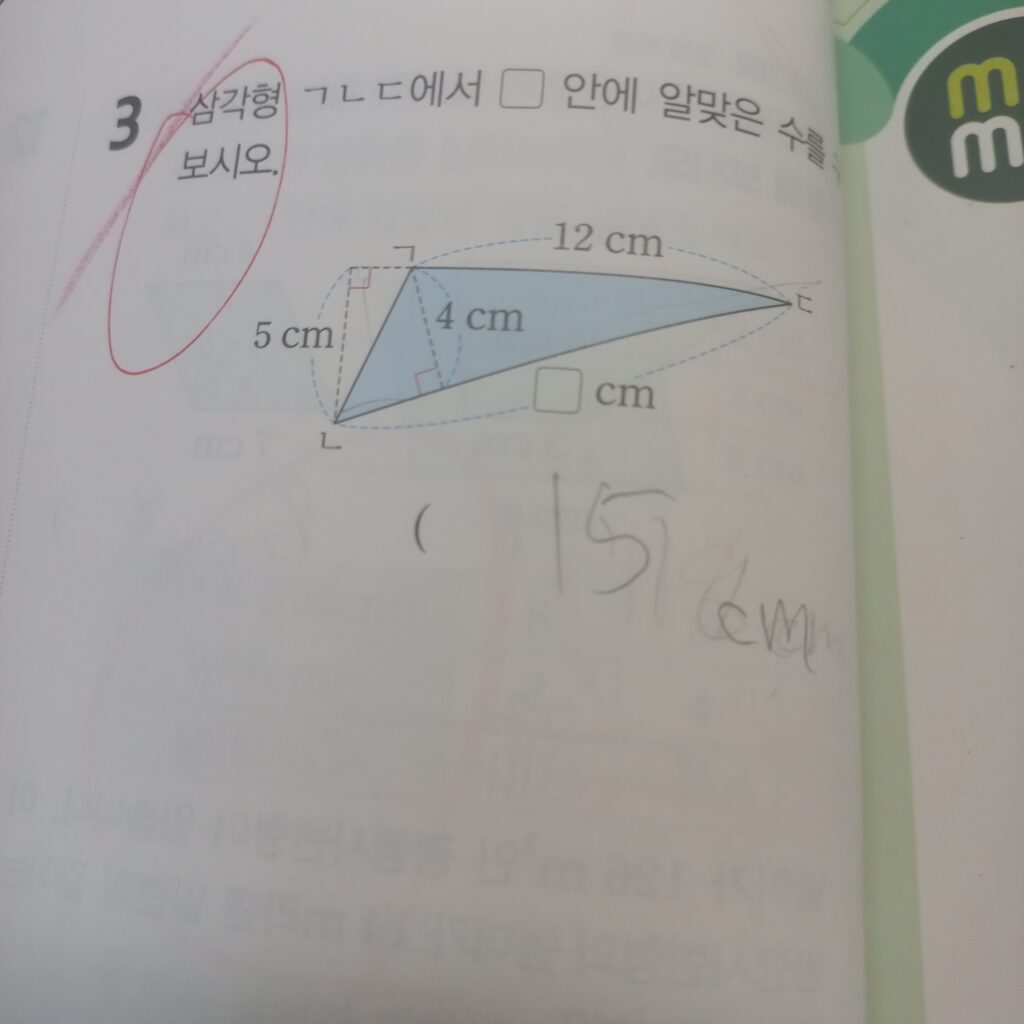
이 문제는 조금 헷갈렸습니다. 만약 네모의 길이를 밑변이라고 본다면 높이는 4센치가 될 것입니다.
삼각형의 넓이를 구하는 식은 예를 들면
3곱하기 4나누기 2는 6입니다.
그러므로 식은 네모 곱하기 4 나누기 2는 30 네모 곱하기 4는 60
60나누기 4는 15 그러므로 답은 15이다.
앞으로 이렇게 틀린 문제는 블로그에 정리할 예정이니 참고하셔도 좋습니다.